虚拟 dom 之更新 (opens new window) 中我们假设了 dom 的结构没有发生变化,完成了 dom 属性和内容的更新。这篇文章,我们假设 dom 没有出现增减,只是发生了移动,看一下这种情况下的更新情况。
# dom 结构
虚拟 dom 之更新 (opens new window) 中我们介绍了不管是 dom 还是虚拟 dom 都是一个 tree 结构。
我们假设每一个节点都是一个 div 节点,叶子节点都是文本节点,每个节点写一个名字方便观察树的变化。
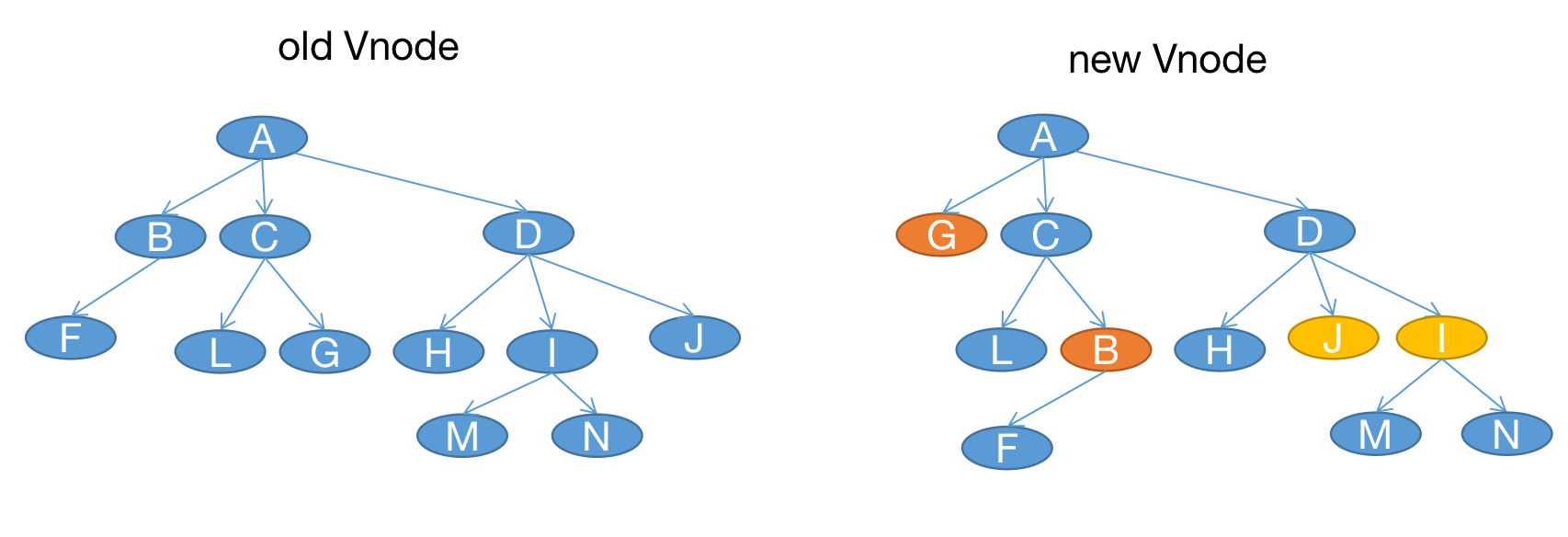
如果 dom 的位置发生了变化,为了复用原有的 dom,我们需要双层遍历,找到新的 vnode 中对应的旧 vnode ,然后从旧 vnode 中拿到 dom 对象进行更新。
for(const newVNode of newVnodeTree) {
for(const oldVNode of oldVnodeTree) {
if(isSameNode(newVNode, oldVNode)) {
newVNode.elm = oldVNodo.elm // 拿到对应的 dom
update(newVNode, oldVNode)
break;
}
}
}
结合图和代码,B 节点和 G 节点发生了交换,如果 G 节点想复用原来的 dom 的节点,就需要遍历 oldVnode 来找到 G 节点,找到之后需要调用 update 函数来更新 G 节点。
我们事前并不知道哪些节点位置发生了变化,所以要依次遍历 newVNode 的所有节点去寻找对应的 OldVNode ,找到后拿到保存在 vnode 的中 dom 节点进行 update 。
update 函数需要去拿到他们各自的父节点和邻居节点,然后进行更新,时间复杂度可能是 O(n) ,再结合外层的两个 for 循环,整体的时间复杂度将是 O()。即使 update 函数非常优秀,那么整体的时间复杂度也一定是大于 O() 的。
如果虚拟 dom 比较大,这个时间复杂度是我们所不能接受的。
我们需要进行一些折中,我们不追求所有 dom 都可以进行复用,我们将复用范围缩小至同一层级的 Children 节点上,如下图红框所示:
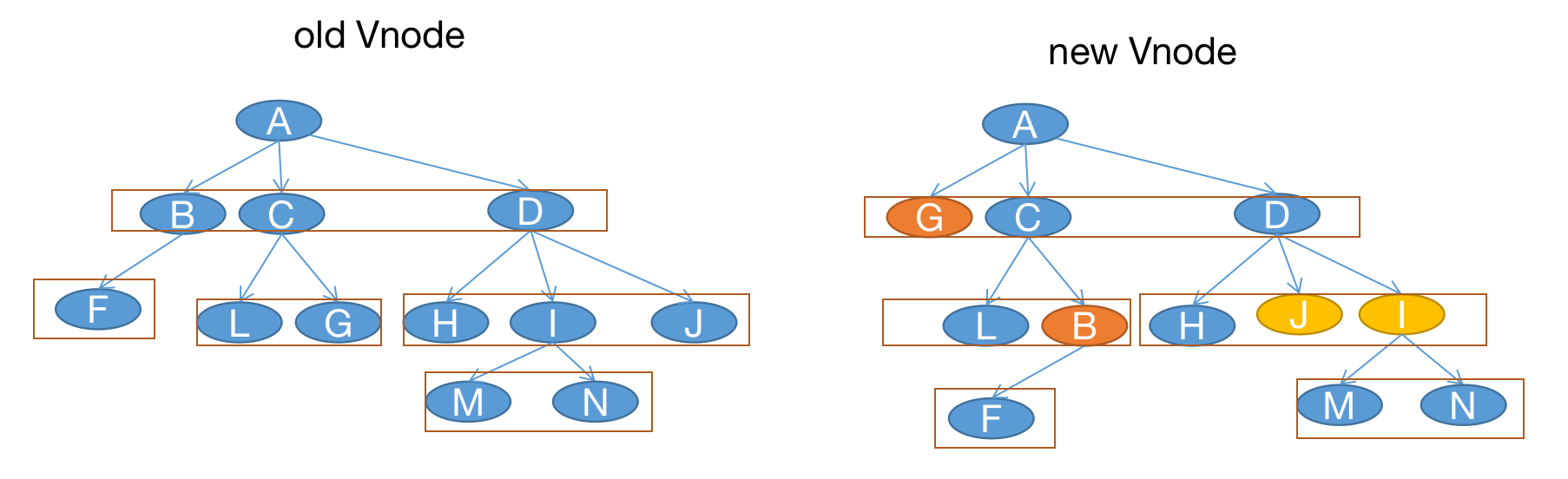
代码就可以改成下边的样子:
for(const newVNode of newVnodeTree) {
const oldVNodo = 从当前节点的同层节点中寻找旧vnode(newVnode)
if(oldVNodo) {
newVNode.elm = oldVNodo.elm
update(newVNode, oldVNode)
}
}
结合图和代码,当我们更新 G 节点的时候,在左图中,它的同层节点也就是 A 的孩子节点是 B、C、D,没有 G 节点,因此 G 节点进行重新生成,不进行复用。
更新 J 节点的时候,它的同层节点是 H、I、J,此时就可以找到相应的 dom 节点进行复用。
我们再考虑一下当前算法的时间复杂度。
首先肯定所有的节点都会遍历一遍,是 O(n),内部分为「从同层节点中寻找节点」和「 update 节点」两部分。
因为同层节点是一个节点的 Children 节点,一般情况下 Children 节点个数相对于树的整个节点个数不会很多,可以看做常数,所以从同层节点中寻找节点可以看做 O(1) 的操作。
再看 update 操作,同样是在同一节点下的 Children 节点中进行,父节点和邻居节点都很好拿到,因此也可以看做 O(1) 的操作。
最终 ,整体上虚拟的 dom 的更新就降为 O(n) 了。
# 更新过程
代码的话主要是接 虚拟 dom 之更新 (opens new window) 来完善。
回忆一下 patchVnode 函数。
function patchVnode(oldVnode, vnode) {
if (oldVnode === vnode) {
return;
}
const elm = (vnode.elm = oldVnode.elm);
const oldCh = oldVnode.children;
const ch = vnode.children;
const data = vnode.data;
if (isDef(data) && isPatchable(vnode)) {
for (i = 0; i < cbs.update.length; ++i)
cbs.update[i](oldVnode, vnode);
}
if (isUndef(vnode.text)) {
if (isDef(oldCh) && isDef(ch)) {
if (oldCh !== ch) updateChildren(elm, oldCh, ch);
} else if (isDef(oldVnode.text)) {
// 更新成了空字符
nodeOps.setTextContent(elm, "");
}
} else if (oldVnode.text !== vnode.text) {
nodeOps.setTextContent(elm, vnode.text);
}
}
如果子节点存在,就调用 updateChildren 方法进行更新子节点。
function updateChildren(elm, oldCh, ch) {
for (let i = 0; i < oldCh.length; i++) {
patchVnode(oldCh[i], ch[i]);
}
}
我们之前假设 dom 节点完全没有变化,所以就直接一一对应进行 patchVnode 。
这篇文章的话,因为我们假设了顺序可能发生变化,因此我们遍历新的 vnode 的后需要找到对应的旧 vnode 。
function updateChildren(elm, oldCh, ch) {
for (let i = 0; i < ch.length; i++) {
for(let j = 0; j < oldCh.length; j++) {
if(sameVnode(ch[i], oldCh[j])) {
ch[i].elm = oldCh[j].elm;
patchVnode(oldCh[i], ch[j]);
break;
}
}
}
}
其中 sameVnode 判断函数如下:
// vue 源码中的 sameVnode 判断的比较多,这里我们仅简单理解为 key、tag 一致,并且 data 属性还存在即可
function sameVnode(a, b) {
return (
a.key === b.key && a.tag === b.tag && isDef(a.data) === isDef(b.data)
);
}
如果我们不设置 vnode 的 key ,第一个条件 a.key === b.key 就是 undefind === undefind ,一定是 true ,这就可能导致本来能够复用的 dom 没有复用上,如下图所示:

当我们遍历 newVnode 的第 0 个节点的时候,由于 vnode 没有设置 key ,直接和 oldVnode 的第 0 个节点匹配到了,但这两个 vnode 其实并不能完全复用,这虽然不会影响到最终的渲染结果,但降低了渲染的性能。
一般情况下我们不设置 key 或者将 key 设置为循环的 index 下标不会影响到最终的渲染结果,但少数特定情况下会出现非预期的结果,此时我们需要考虑是否通过添加、修改 key 来解决。
回到我们的 updateChildren 函数:
function updateChildren(elm, oldCh, ch) {
for (let i = 0; i < ch.length; i++) {
for(let j = 0; j < oldCh.length; j++) {
if(sameVnode(ch[i], oldCh[j])) {
ch[i].elm = oldCh[j].elm;
patchVnode(oldCh[i], ch[j]);
break;
}
}
}
}
假设我们设置了 key ,成功找到了对应的 vnode ,但上边的代码还不够,上边的代码相当于只是把 dom 更新了,但是顺序还没有改变,如下图所示,第 0 个第 2 个节点的叶子节点的 text 更新了。
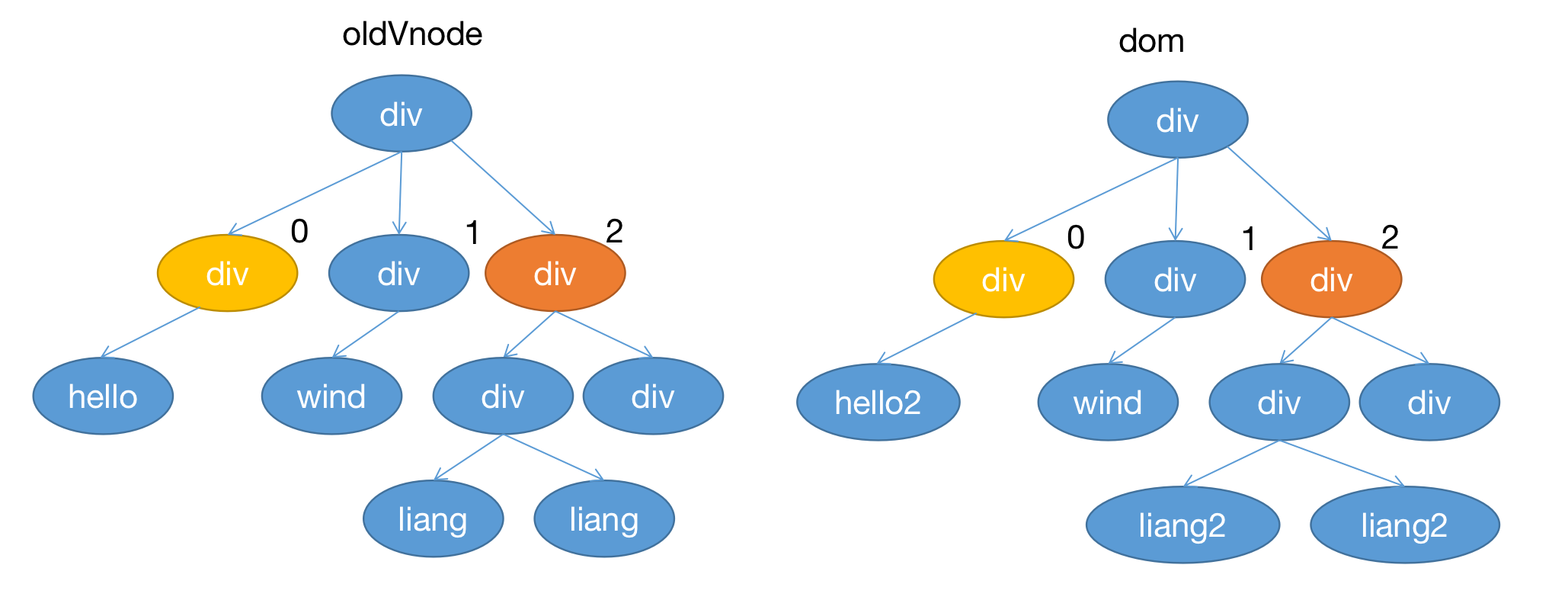
但是我们当前的 vnode 结构如下:
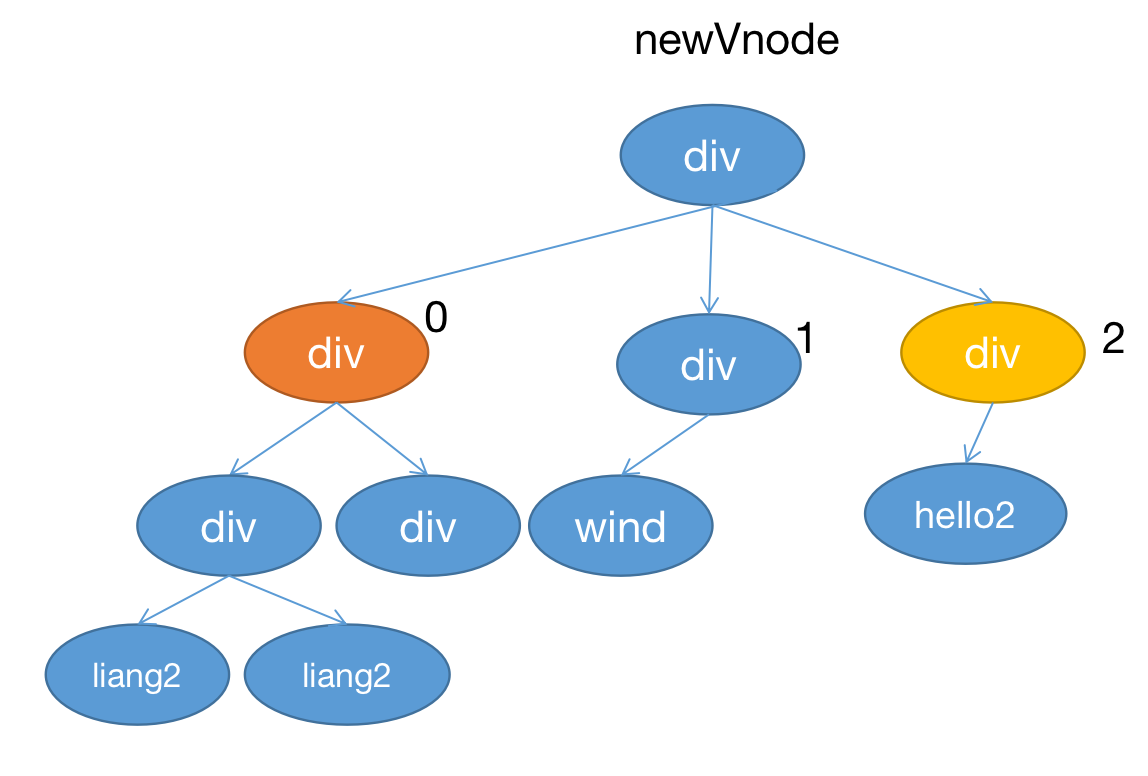
橙色节点和黄色节点位置进行了交换,因此我们还需要添加 dom 移动的代码。
# diff 算法
这里就需要设计一个算法,来理清什么情况下该移动 dom ,什么情况下不该移动 dom 。
假设原来的顺序是 a、b、c、d、e,新的顺序是 a、e、b、c、d。
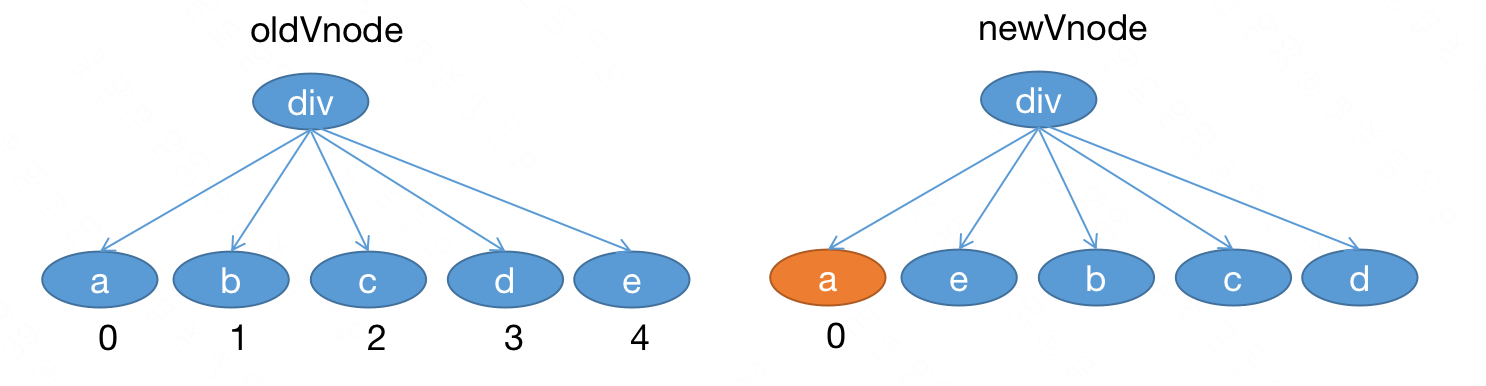
我们开始遍历 newVnode ,遍历到 a ,当前只有一个,不需要考虑顺序。
# 遍历到 e :

newVnode 中 e 在 a 的后边, a 对应原来的位置是 0,e 对应原来的位置是 4 ,说明原来 e 也在 a 后边,此时无需移动。
# 遍历到 b:
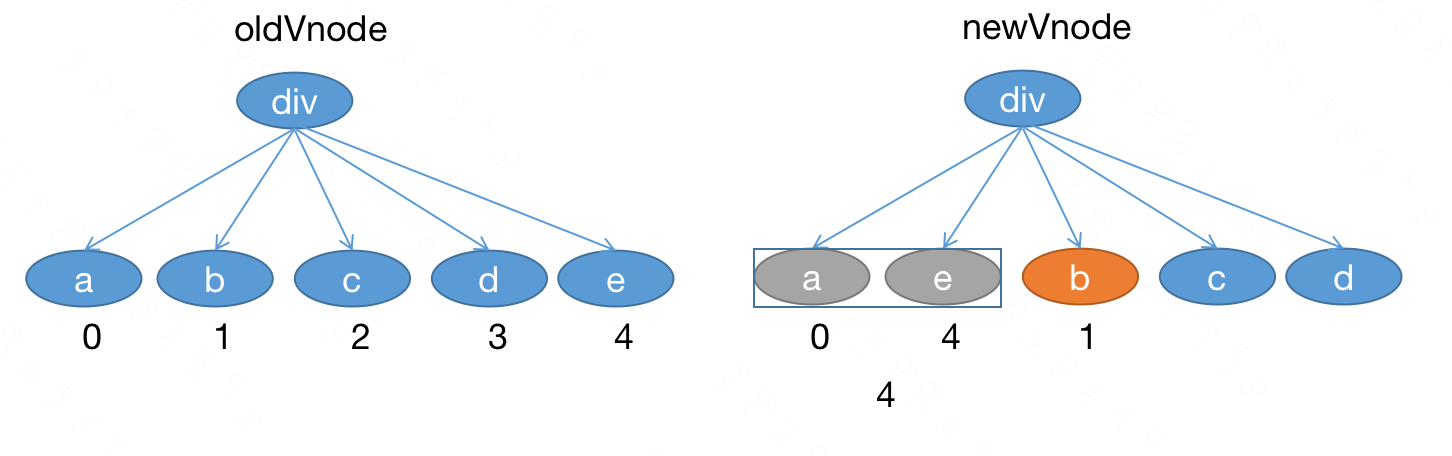
newVnode 中 b 此时在 a 和 e 的后边,如果 b 不用移动,那么 b 对应的原来的位置应该比 a、e 对应的原来的位置都要大。
但 a 对应的原来位置是 0 ,e 对应的原来的位置是 4 ,较大的位置是 4,b 对应的原来的位置是 1 小于 4,说明 b 之前在 a 或者 e 的前边。
此时需要移动,移动到哪里?拿到 b 的前一个节点 e ,然后接到后边即可。
当前 dom 顺序变化:
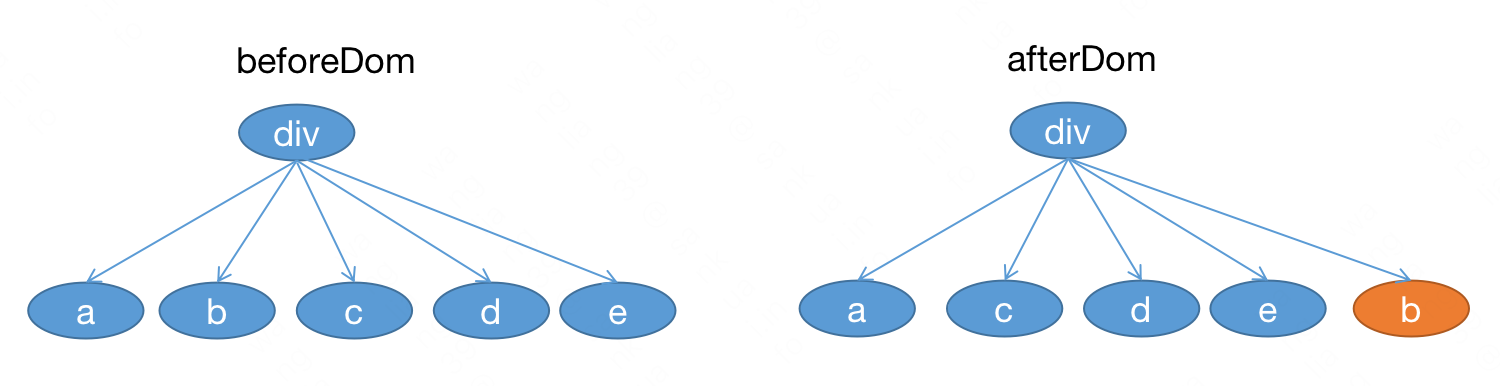
# 遍历到 c :
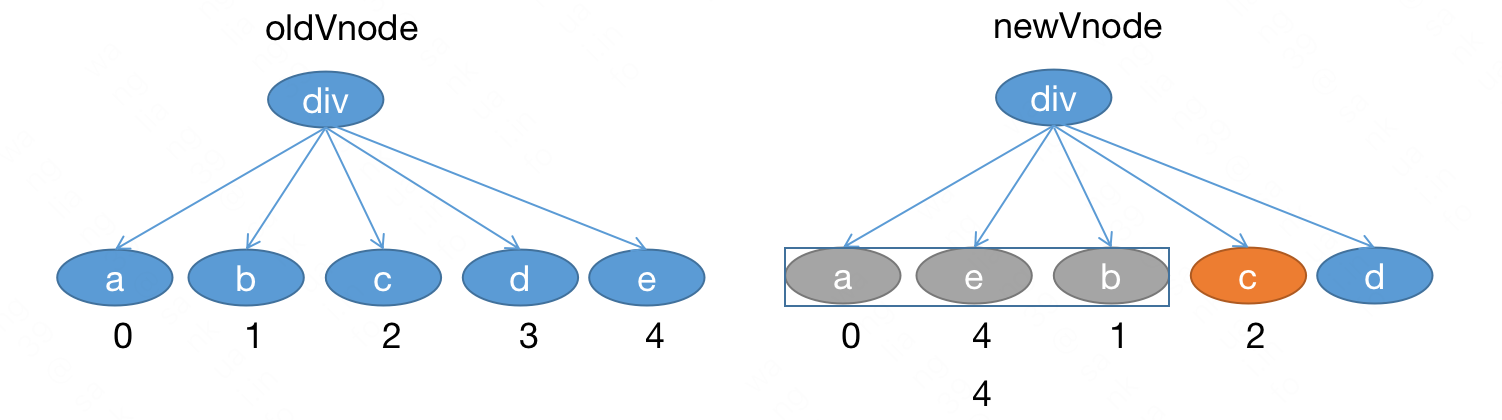
c 此时在 a 、e 和 b 的后边,如果 c 不用移动,那么 c 对应的原来的位置应该比 a、e 、b 对应的原来的位置都要大。
但 a 对应的原来位置是 0 ,e 对应的原来的位置是 4 ,b 对应的原来的位置是 1,最大的位置是 4,c 对应的原来的位置是 2 小于 4,说明 c 之前在 a 或者 e 或者 b 的前边。
此时 c 需要移动,移动到哪里?拿到 c 的前一个节点 b ,然后接到后边即可。
当前 dom 顺序变化:

# 遍历到 d :
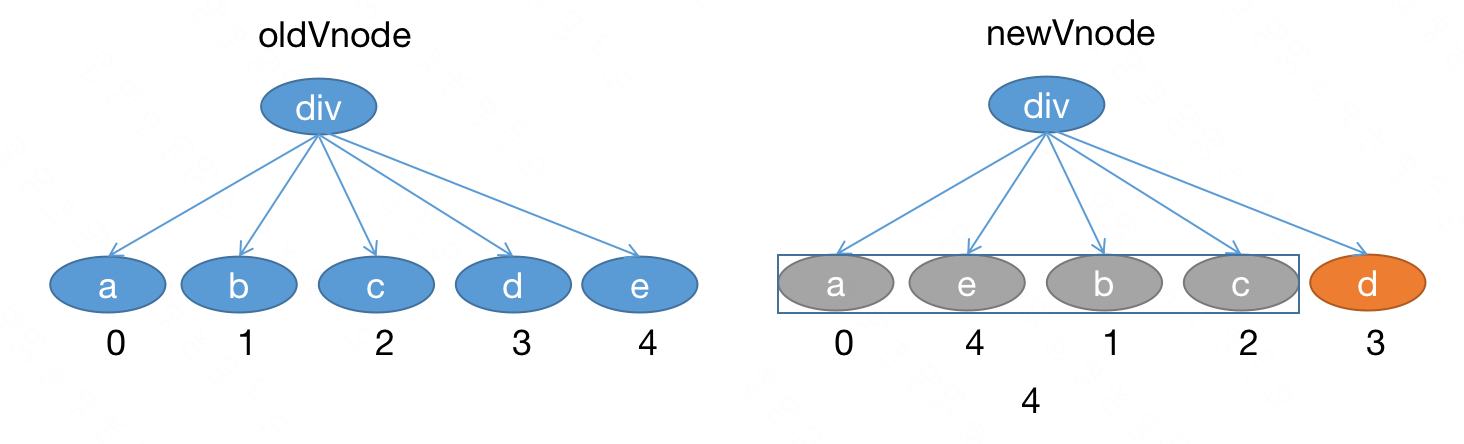
d 此时在 a 、e、b 和 c 的后边,如果 d 不用移动,那么 d 对应的原来的位置应该比 a、e 、b 、c 对应的原来的位置都要大。
但 a 对应的原来位置是 0 ,e 对应的原来的位置是 4 ,b 对应的原来的位置是 1,c 对应的原来的位置是 2,最大的位置是 4,d 对应的原来的位置是 3 < 最大位置 4 ,说明 d 之前在 a 或者 e 或者 b 或者 c 的前边。
此时 d 需要移动,移动到哪里?拿到 d 的前一个节点 c ,然后接到后边即可。
当前 dom 顺序变化:
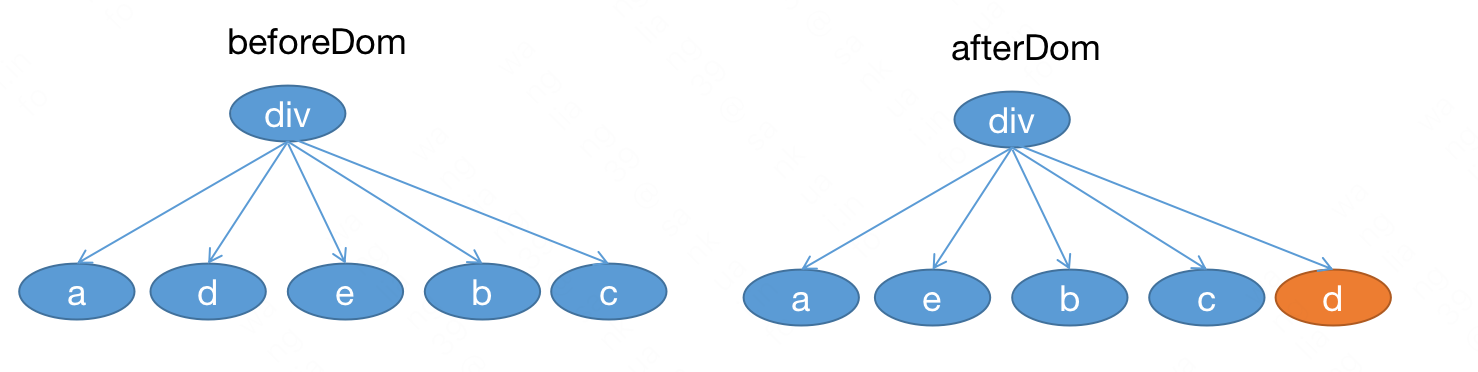
可以看到此时 dom 的顺序就和 new Vnode 的顺序一致了。
# 算法总结
我们通过当前节点和前边所有节点对应的原位置的大小来判断它们的相对关系需不需要变化,如果变化我们就接到前一个节点的后边(保证它们的绝对位置关系正确),最终实现了正确的排序。
算法过程如下:
保存当前已经排好序的节点列表中对应的 oldVnode 的最大位置,然后比较当前遍历的节点对应的原来的位置和前边的最大位置。
如果当前对应的位置大于最大位置,那就说明顺序正常无需移动,然后更新排好序节点列表 dom 的最大位置。
如果当前对应的位置小于最大位置,说明当前节点位置需要移动,我们只需要接到它的前一个节点后边即可。
对应到代码就是下边的样子了:
function updateChildren(elm, oldCh, ch) {
let beforeMaxIndex = -1;
for (let i = 0; i < ch.length; i++) {
for (let j = 0; j < oldCh.length; j++) {
if (sameVnode(ch[i], oldCh[j])) {
ch[i].elm = oldCh[j].elm;
patchVnode(oldCh[j], ch[i]);
// 移动位置
if (i > beforeMaxIndex) {
// 无需移动
beforeMaxIndex = j;
} else {
const currentVnode = ch[i];
const beforeVnode = ch[i - 1];
nodeOps.insertBefore(
elm,
currentVnode.elm,
nodeOps.nextSibling(beforeVnode.elm)
);
}
break;
}
}
}
}
当然,因为有key 的存在,我们还可以继续优化一下代码,将 oldCh 通过 key 映射为一个 map ,通过 key 直接拿到 oldCh 对应的下标,这样就不需要每次都进行一次 for 循环去遍历 oldCh 了。
function createKeyToOldIdx(children, beginIdx, endIdx) {
let i, key;
const map = {};
for (i = beginIdx; i <= endIdx; ++i) {
key = children[i].key;
if (isDef(key)) map[key] = i;
}
return map;
}
// 没有 key 的话还是 for 循环
function findIdxInOld(node, oldCh, start, end) {
for (let i = start; i < end; i++) {
const c = oldCh[i];
if (isDef(c) && sameVnode(node, c)) return i;
}
}
function updateChildren(elm, oldCh, ch) {
let beforeMaxIndex = -1;
let oldKeyToIdx, idxInOld;
for (let i = 0; i < ch.length; i++) {
const newVnode = ch[i];
if (isUndef(oldKeyToIdx)) // 是否已经映射过了
oldKeyToIdx = createKeyToOldIdx(oldCh, 0, oldCh.length - 1);
idxInOld = isDef(newVnode.key)
? oldKeyToIdx[newVnode.key] // 有 key 直接映射
: findIdxInOld(newVnode, oldCh, 0, oldCh.length); // 没有 key 的情况
if (sameVnode(newVnode, oldCh[idxInOld])) {
newVnode.elm = oldCh[idxInOld].elm;
patchVnode(oldCh[idxInOld], ch[i]);
// 移动位置
if (i > beforeMaxIndex) {
// 无需移动
beforeMaxIndex = idxInOld;
} else {
const currentVnode = newVnode;
const beforeVnode = ch[i - 1];
nodeOps.insertBefore(
elm,
currentVnode.elm,
nodeOps.nextSibling(beforeVnode.elm)
);
}
}
}
# 测试
我们在 render 中渲染一个数组,然后点击的时候改变数组中元素的位置:
import * as nodeOps from "./node-ops";
import modules from "./modules";
import { createPatchFunction } from "./patch";
import { createElement } from "./create-element";
import { observe } from "./observer/reactive";
import Watcher from "./observer/watcher";
const options = {
el: "#root",
data: {
list: ["a", "b", "c"],
},
render(createElement) {
const children = [];
for (const item of this.list) {
children.push(createElement("div", { key: item }, item));
}
const vnode = createElement(
"div",
{
on: {
click: () => {
console.log(1);
this.list = ["c", "b", "a"];
},
},
},
children
);
return vnode;
},
};
const _render = function () {
const vnode = options.render.call(options.data, createElement);
return vnode;
};
const __patch__ = createPatchFunction({ nodeOps, modules });
const vm = {};
vm.$el = document.querySelector(options.el);
const _update = (vnode) => {
const prevVnode = vm._vnode;
vm._vnode = vnode;
// Vue.prototype.__patch__ is injected in entry points
// based on the rendering backend used.
if (!prevVnode) {
// initial render
vm.$el = __patch__(vm.$el, vnode);
} else {
// updates
vm.$el = __patch__(prevVnode, vnode);
}
};
observe(options.data);
new Watcher(options.data, () => _update(_render()));
看一下效果:

dom 顺序成功进行了更新。
# 总
这篇文章主要介绍了 diff 算法从 降为 的核心思想,然后详细介绍了简单的 diff 算法,在假设 dom 节点没有增删的情况下对 dom 进行了移动。
Vue2 中对上边的 diff 算法进行了进一步的优化,下篇文章继续。